1. Bisection
VC2M10AA02: level 10A: Devise and use algorithms and simulations to solve mathematical problems
Applying a systematic guess-check-and-refine algorithm to identify an approximate value for the root of an equation in an interval
1.1. The Bisection method
The bisection method is an algorithms that can be used to approximate the roots of a function.
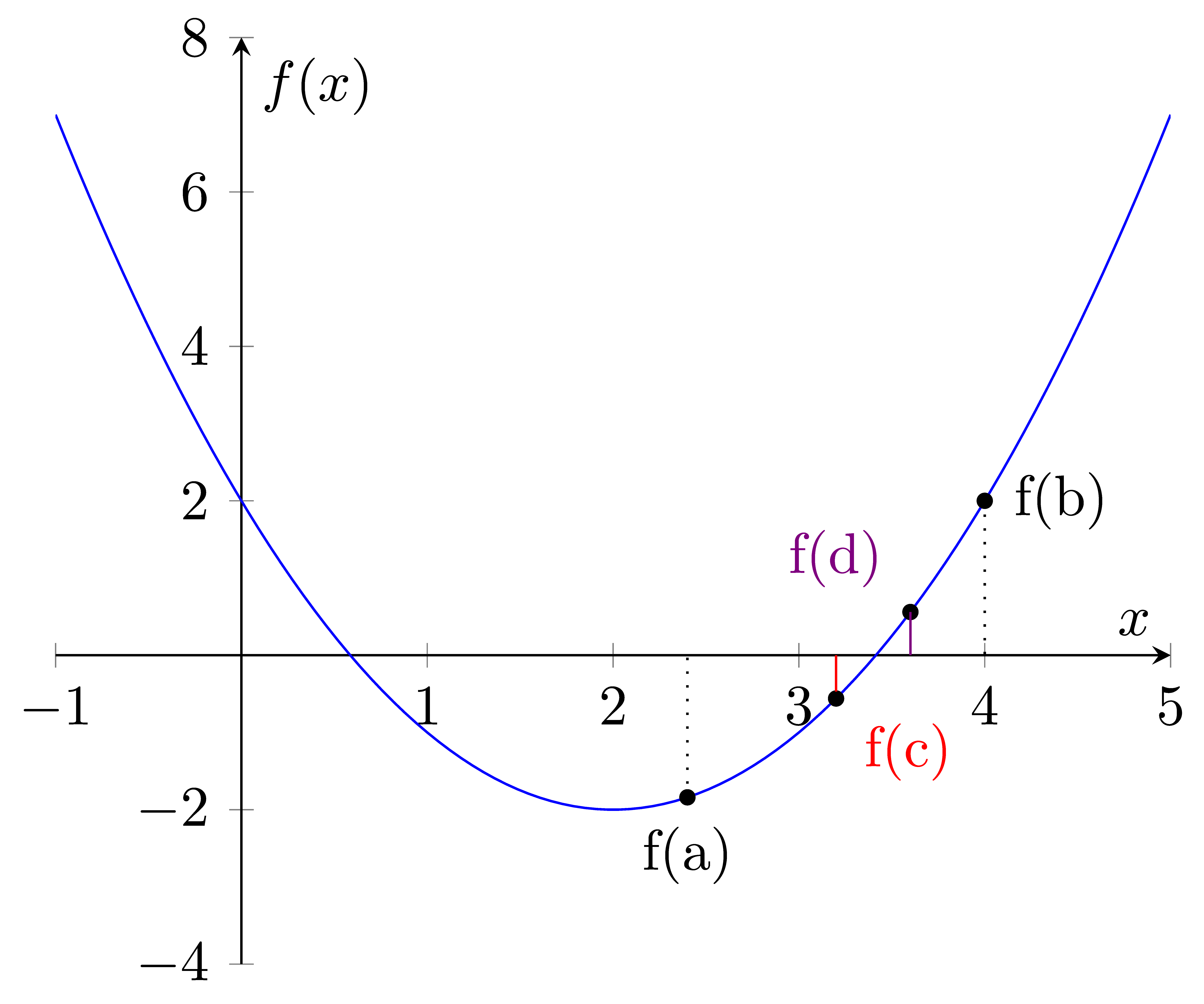
The bisection method works by repeatedly dividing an interval in half and checking which half contains a root.
The method starts with an interval [a,b] such that f(a) and f(b) have opposite signs, which means that there must be at least one root in the interval.
The midpoint of the interval is calculated as c = (a + b) / 2, and the function is evaluated at this point.
If f(c) is zero, then c is a root of the function. Otherwise, the sign of f(c) is compared to the sign of f(a) and f(b).
If f(c) has the same sign as one of the endpoints, then the root must be in the other half of the interval, so the interval is updated accordingly.
This process is repeated until a sufficiently accurate approximation of the root is found.
It’s important to choose an appropriate initial interval or initial guess and to monitor the convergence of the method to ensure that it’s providing accurate results.
1.2. Bisection with specified Iterations
Pseudocode for the bisection method is below.
This code defines a function bisection that takes four arguments: f, a, b, and max_iter.
The function checks if the product of f(a) and f(b) is greater than 0. If it is, it returns “Invalid interval”.
Otherwise, it enters a while loop that iterates max_iter times.
During each iteration, the code calculates the midpoint between a and b and checks if f(mid) is equal to 0.
If it is, the function returns mid.
If not, the code checks if the product of f(a) and f(mid) is less than 0.
If it is, the value of b is updated to be equal to mid.
Otherwise, the value of a is updated to be equal to mid.
The loop counter i is then incremented by 1.
After the loop has completed, the function returns the final value of mid.
Pseudocode:
define bisection (f(x), a, b, max_iter)
if f(a) x f(b) > 0 then
return “Invalid interval”
i ← 0
while i < max_iter
mid ← (a + b) ÷ 2
if f(mid) = 0 then
return mid
else if f(a) x f(mid) < 0 then
b ← mid
else
a ← mid
i ← i + 1
end while
return mid
Python implementation:
def bisection(f, a, b, max_iter):
if f(a) * f(b) > 0:
return "Invalid interval"
i = 0
while i < max_iter:
mid = (a + b) / 2
if f(mid) == 0:
return mid
elif f(a) * f(mid) < 0:
b = mid
else:
a = mid
i += 1
return mid
1.3. Cubic Example
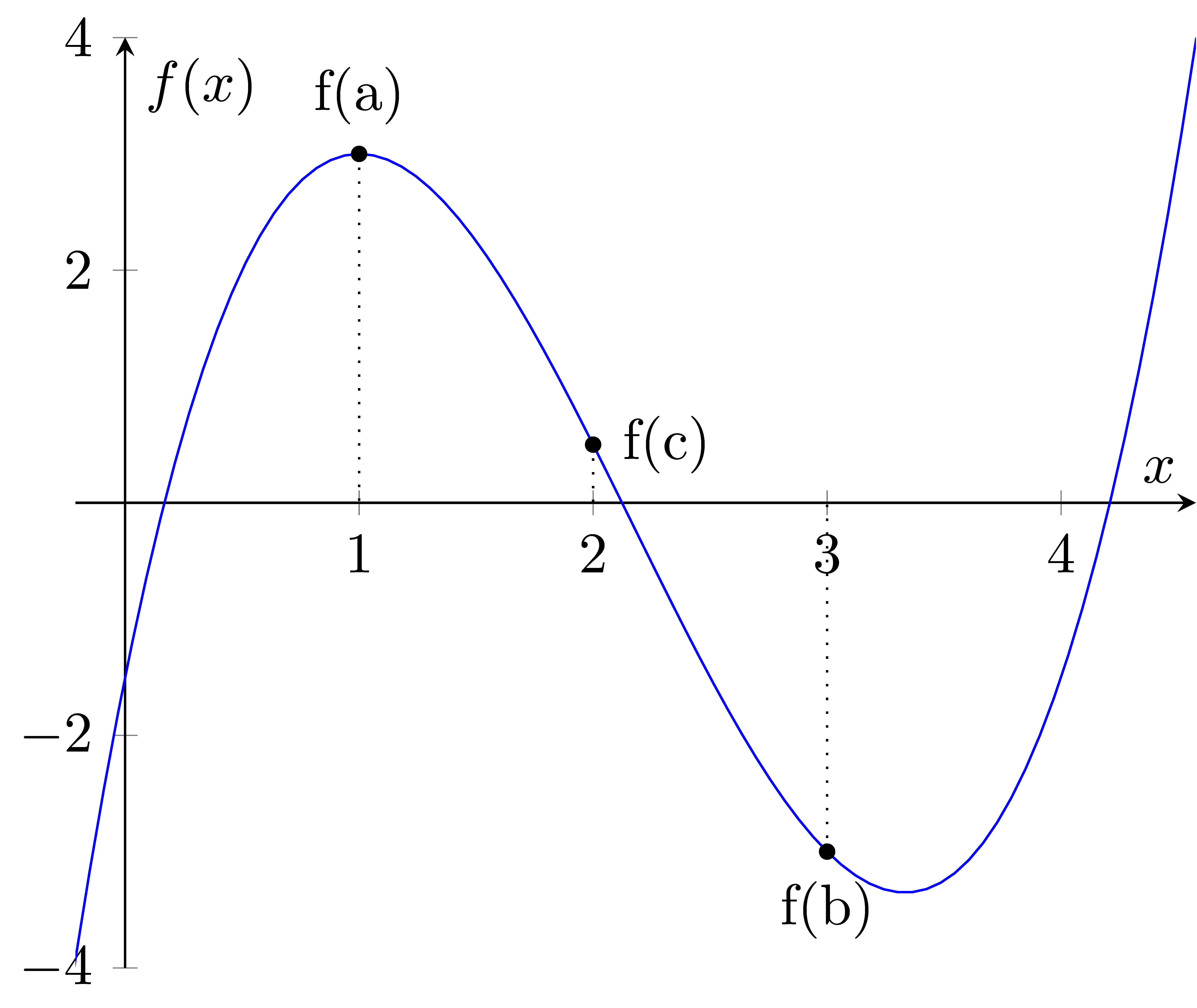
Here’s an example of how you can use the bisection function to find the root of a cubic function in the interval [1, 3] with a maximum of 10 Iterations.
The output value is 2.123046875.
def f(x):
return x**3 - 6.5*x**2 + 10*x - 1.5
def bisection(f, a, b, max_iter):
if f(a) * f(b) > 0:
return "Invalid interval"
i = 0
while i < max_iter:
mid = (a + b) / 2
if f(mid) == 0:
return mid
elif f(a) * f(mid) < 0:
b = mid
else:
a = mid
i += 1
return mid
bisec_value = bisection(f,1,3,10)
print(bisec_value)
# 2.123046875
1.4. Example with sin function
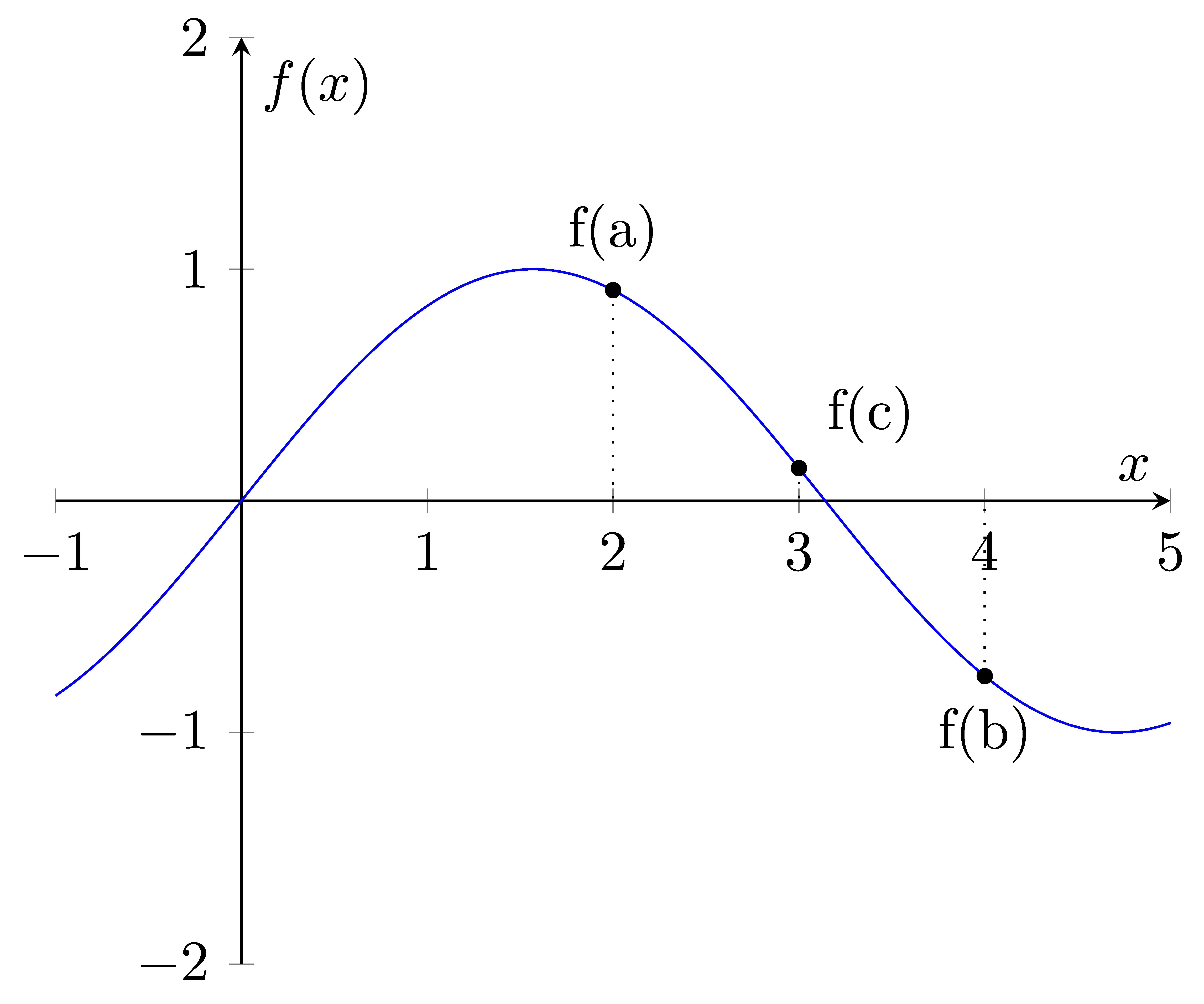
Here’s an example of how you can use the bisection function to find the root of the sin(x) function in the interval [2, 4] with a maximum of 5 Iterations.
The output value is 3.1875.
from math import sin
f = lambda x: sin(x)
def bisection(f, a, b, max_iter):
if f(a) * f(b) > 0:
#need one pos and one neg
return "Invalid interval"
i = 0
while i < max_iter:
mid = (a + b) / 2
if f(mid) == 0:
return mid
elif f(a) * f(mid) < 0:
b = mid
else:
a = mid
i += 1
return mid
bisec_value = bisection(f,2,4,5)
print(bisec_value)
# 3.1875
1.5. Bisection with specified error tolerance
The bisection method can check how close the y value is to zero when estimating the root of the equation and stop when a certain tolerance, max_diff, has been reached.
A print statement is included to output the x and y values at each Iteration.
Pseudocode:
define bisection (f(x), a, b, max_iter, max_diff)
if f(a) x f(b) > 0 then
return “Invalid interval”
i ← 0
while i < max_iter
mid ← (a + b) ÷ 2
print (“Iteration i: a, b, mid, y”)
if abs(f(mid)) <= max_diff then
return mid
else if f(a) x f(mid) < 0 then
b ← mid
else
a ← mid
i ← i + 1
end while
return mid
Python implementation:
def bisection(f, a, b, max_iter, max_diff):
if f(a) * f(b) > 0:
return "Invalid interval"
i = 0
while i < max_iter:
mid = (a + b) / 2
print('Iteration {:2d}: a={:.10f}, b={:.10f}, mid={:.10f}, y={: .10f}'.format (i, a, b, mid, f(mid)))
if abs(f(mid)) <= max_diff:
return mid
elif f(a) * f(mid) < 0:
b = mid
else:
a = mid
i += 1
return mid
1.6. Cubic Example
Here’s an example of how you can use the bisection function to find the root of a cubic function in the interval [1, 3] with a maximum error in the y value of 0.0001.
The output value is 2.12353515625.
def f(x):
return x**3 - 6.5*x**2 + 10*x - 1.5
def bisection(f, a, b, max_iter, max_diff):
if f(a) * f(b) > 0:
return "Invalid interval"
i = 0
while i < max_iter:
mid = (a + b) / 2
print('Iteration {:2d}: a={:.10f}, b={:.10f}, mid={:.10f}, y={: .10f}'.format (i, a, b, mid, f(mid)))
if abs(f(mid)) <= max_diff:
return mid
elif f(a) * f(mid) < 0:
b = mid
else:
a = mid
i += 1
return mid
bisec_value = bisection(f,1,3,100,0.0001)
print(bisec_value)
# 2.12353515625
Table of values:
Iteration 0: a=1.0000000000, b=3.0000000000, mid=2.0000000000, y= 0.5000000000
Iteration 1: a=2.0000000000, b=3.0000000000, mid=2.5000000000, y=-1.5000000000
Iteration 2: a=2.0000000000, b=2.5000000000, mid=2.2500000000, y=-0.5156250000
Iteration 3: a=2.0000000000, b=2.2500000000, mid=2.1250000000, y=-0.0058593750
Iteration 4: a=2.0000000000, b=2.1250000000, mid=2.0625000000, y= 0.2482910156
Iteration 5: a=2.0625000000, b=2.1250000000, mid=2.0937500000, y= 0.1214294434
Iteration 6: a=2.0937500000, b=2.1250000000, mid=2.1093750000, y= 0.0578269958
Iteration 7: a=2.1093750000, b=2.1250000000, mid=2.1171875000, y= 0.0259928703
Iteration 8: a=2.1171875000, b=2.1250000000, mid=2.1210937500, y= 0.0100688338
Iteration 9: a=2.1210937500, b=2.1250000000, mid=2.1230468750, y= 0.0021052286
Iteration 10: a=2.1230468750, b=2.1250000000, mid=2.1240234375, y=-0.0018769512
Iteration 11: a=2.1230468750, b=2.1240234375, mid=2.1235351562, y= 0.0001141696
Iteration 12: a=2.1235351562, b=2.1240234375, mid=2.1237792969, y=-0.0008813832
Iteration 13: a=2.1235351562, b=2.1237792969, mid=2.1236572266, y=-0.0003836049
Iteration 14: a=2.1235351562, b=2.1236572266, mid=2.1235961914, y=-0.0001347172
Iteration 15: a=2.1235351562, b=2.1235961914, mid=2.1235656738, y=-0.0000102737